– – – – – – – – – – – – – – – – – – – – – –

#FTScienceWeek

ഹൈസ്കൂൾ ക്ലാസുകളിൽ എല്ലാവരും ജോമെട്രി പഠിച്ചിട്ടുണ്ടാവുമല്ലോ. ജോമെട്രിയുടെ പിതാവ് ബി സി 300 നോടടുത്ത് ഗ്രീസിൽ ജീവിച്ചിരുന്ന യൂക്ലിഡ് എന്ന ഗണിത ശാസ്ത്രജ്ഞനാണ്. ഇദ്ദേഹമാണ് ജോമെട്രിയെ സംബന്ധിച്ച ആധികാരിക ഗ്രന്ഥമായ എലമെന്റ്സ് എഴുതിയത്. ഇപ്പോഴും ഇതിലെ പല ഭാഗങ്ങളും നാം ഗണിത ക്ലാസുകളിൽ പഠിക്കാറുണ്ട്.

യൂക്ലിഡിന്റെ ജോമെട്രി പ്രധാനമായും അഞ്ച് പോസ്റ്റുലേറ്റുകളെ അടിസ്ഥാനമാക്കിയാണ് രേഖപ്പെടുത്തിയിരിക്കുന്നത്.

നമുക്ക് ആദ്യം ഗണിത ശാസ്ത്രത്തിൽ പോസ്റ്റുലേറ്റ് (postulate) അഥവാ ഓക്സിയം (axiom) എന്ന പദം കൊണ്ട് എന്താണ് അർത്ഥമാക്കുന്നതെന്ന് നോക്കാം.

പ്രത്യേകിച്ച് തെളിവ് (Proof) ഇല്ലാതെ തന്നെ സത്യമാണെന്ന് (true ) മുൻകൂട്ടി നിശ്ചയിച്ചിട്ടുള്ള ഒരു പ്രസ്താവനയാണ്. ഇത്തരം പല പോസ്റ്റുലേറ്റുകളും നാം നിത്യജീവിതത്തിൽ ഉപയോഗിക്കുന്നുണ്ട്. ഉദാഹരണത്തിന് പൂജ്യം എന്ന ഒരു സംഖ്യയുണ്ട് എന്ന് നാം നിർവചിച്ചു വെച്ചിട്ടുണ്ട്. ഇത്തരം പോസ്റ്റുലേറ്റുകളാണ് പല ശാസ്ത്ര ശാഖകളുടേയും അടിസ്ഥാനം. ഇവ സത്യമാണെന്ന് (true) നമുക്ക് ഉറപ്പുണ്ട്.

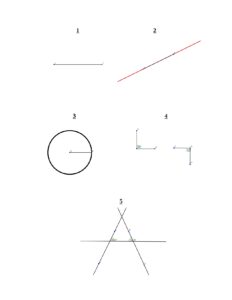
ജോമട്രിയുടെ അടിസ്ഥാന തത്വങ്ങളായ യൂക്ലിഡിന്റെ അഞ്ച് പോസ്റ്റുലേറ്റുകളെ വിശദീകരിക്കാൻ ശ്രമിക്കുകയാണ് ഈ കുറിപ്പ്. യൂക്ലിഡിയൻ ജോമെട്രിയുടെ അടിസ്ഥാന പ്രമാണങ്ങളാണ് ഈ അഞ്ചും. കാര്യങ്ങൾ വ്യക്തമായി മനസ്സിലാക്കാൻ ഇതോടൊപ്പമുള്ള ചിത്രം കൂടി നോക്കുമല്ലോ. ഇനി നമുക്ക് കാര്യത്തിലേക്ക് കടക്കാം.

1 എത് രണ്ട് ബിന്ദുക്കൾ തമ്മിലും ഒരു നേർരേഖ വരക്കാം. ചിത്രത്തിൽ 1 എന്ന് ഇത് രേഖപ്പെടുത്തിയിട്ടുണ്ട്‌.
ഇത് നാം ജീവിതത്തിൽ നിത്യേന എന്നോണം ഉപയോഗിക്കുന്ന തത്വമാണ്. ഈ പോസ്റ്റുലേറ്റ് നാമറിയാതെ തന്നെ ജീവിതത്തിൽ എന്നും ഉപയോഗിക്കുന്നു. ഒന്ന് ആലോചിച്ച് നോക്കൂ.

2 ഏതൊരു നേർരേഖയുടെ കഷ്ണത്തേയും. (line segment) അനന്തമായ ഒരു നേർരേഖയായി വികസിപ്പിക്കാം. ചിത്രത്തിൽ 2 എന്ന് ഇതിനെ അടയാളപ്പെടുത്തിയിട്ടുണ്ട് . ഇതും നാം എന്നും ഉപയോഗിക്കുന്നുണ്ട്. ആലോചിച്ച് നോക്കിയാൽ സത്യമാണെന്ന് കാണാം.

3 നിശ്ചിത നീളമുള്ള ഒരു നേർരേഖ ഉണ്ടെന്നിരിക്കട്ടെ, ഈ വരയുടെ നീളം ആരമായിട്ടുള്ള ഒരു വൃത്തം രേഖയുടെ ഒരറ്റം കേന്ദ്രമായി വരക്കാൻ പറ്റും. കുട്ടികൾ കോമ്പസ് ഉപയോഗിച്ച് വൃത്തം വരയ്ക്കുന്നത് ഇങ്ങനെയാണ്.

4 സമകോണുകൾ ( Right angle )എല്ലാം സർവ്വസമമാണ് (congruent)
സമകോൺ എന്താണെന്ന് നമുക്കെല്ലാം അറിയാം. ചിത്രത്തിൽ 4 എന്ന് കാണിച്ചിരിക്കുന്നത് രണ്ട് സമകോണുകളാണ്. ഇനി എന്താണ് കോൺഗ്രുവൻസ് എന്ന് നോക്കാം. ചിത്രത്തിൽ രണ്ട് സമകോണുകൾ വരച്ചിരിക്കുന്നത് കണ്ടു കാണുമല്ലോ. ഒരേ പേലെയുള്ള രണ്ട് ചിത്രങ്ങളാണ് അവ. പക്ഷെ ഒരെണ്ണം ചെരിച്ചാണ് വരച്ചിട്ടുള്ളതെന്നു മാത്രം. ഒന്നാമത്തെ കോണിനെ രണ്ടാമത്തേതിന് അരികിലേക്ക് നീക്കുക. ഇനി ഈ കോണിനെ തിരിച്ച് (rotate) രണ്ടാമത്തേതിന് മുകളിൽ വെക്കുക. ഇപ്പോൾ ഒന്നാമത്തേതും രണ്ടാമത്തേതും തമ്മിൽ പരസ്പരം തിരിച്ചറിയാൻ കഴിയില്ല. അപ്പോൾ ഈ രണ്ട് കോണുകളും സർവ്വസമമാണെന്ന് പറയാം.

5 ) രണ്ടു രേഖകൾ ഉണ്ടെന്നിരിക്കട്ടെ. മൂന്നാമതൊരു നേർരേഖ ഇവ രണ്ടിനോടും കൂട്ടിമുട്ടുന്നു എന്നും വിചാരിക്കുക (ചിത്രത്തിലെ 5 എന്ന ഭാഗം നോക്കുക | ഈ മൂന്നാമൻ മറ്റു രണ്ടു രേഖകളുമായി ഉണ്ടാക്കുന്ന കോണുകളുടെ തുക (ചിത്രത്തിൽ A, B എന്നിങ്ങനെ കാണിച്ചിരിക്കുന്നു. A+B< 180) 180 ഡിഗ്രിയിൽ കുറവാണെങ്കിൽ ,ആ വശത്ത് ആദ്യത്തെ രണ്ട് രേഖകൾ കൂട്ടിമുട്ടും. ചിത്രം കണ്ടാൽ ഇത് കുറേക്കൂടി വ്യക്തമാകും. ഈ അഞ്ചാമനെ പാരലൽ പോസ്റ്റുലേറ്റ് എന്നും വിളിക്കാറുണ്ട്.

പടം ജിയോജിബ്ര യിൽ വരച്ചത് വിദ്യ