നമ്മളെല്ലാം സ്കൂള്‍ കോളേജ് ക്ലാസുകളില്‍ മെട്രിക്സുകളേക്കുറിച്ച് പഠിച്ചിട്ടുണ്ടാകും. സംഖ്യകളുടെ ഒരു നിര എന്നാണ് നമ്മളെ പഠിപ്പിച്ചു വച്ചിരിക്കുന്നത്. മെട്രിക്സുകളെ കൂട്ടാനും കുറക്കാനും ഗുണിക്കാനും പഠിപ്പിക്കും. പക്ഷേ, ഉപയോഗമെന്തെന്ന് ആരും ചിന്തിക്കാറില്ല. ഈയടുത്ത് ഒരു വിദ്യാർത്ഥിയോട്  ഇതിനെക്കുറിച്ച് ചോദിച്ചപ്പോൾ  സംഖ്യകളെ പെട്ടിക്കുള്ളിലാക്കിയതാണ്   മെട്രിക്സ് എന്നാണ് ഉത്തരം പറഞ്ഞത് 🙂

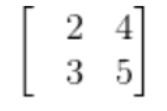
ചിത്രം 1

 

മെട്രിക്സുകളെ എങ്ങിനെയാണ് നമ്മൾ  മനസ്സിലാക്കേണ്ടതെന്ന് വിശദീകരിക്കാൻ ശ്രമിക്കുകയാണ് ഈ കുറിപ്പിൽ സയൻസിലെയും ടെക്നോളജിയിലെയും നാനാ ശാഖകളിൽ മെട്രിക്സുകളെ ഉപയോഗപ്പെടുത്തുന്നുണ്ട്. മെഷീന്‍ലേണിംഗിലും ഡാറ്റാ സയന്‍സിലും  പ്രവർത്തിക്കുന്നവർക്ക് മെട്രിക്സുകളെക്കുറിച്ചും ലീനിയര്‍  ആൾജിബ്ര  എന്ന ഗണിത ശാഖയെക്കുറിച്ചും കുറിച്ചും വ്യക്തമായ ധാരണ വേണം. കമ്പ്യൂട്ടർ സോഫ്റ്റ്‌വെയർ രംഗത്തു പ്രവർത്തിക്കുന്ന പലരും ഇപ്പോൾ  മെഷീൻ ലേണിങ്ങിലേക്ക് ചുവടുമാറാൻ  നോക്കുന്നുണ്ട് . ഇത്തരക്കാർ തീർച്ചയായും ലീനിയർ ആൾജിബ്ര  പഠിച്ചിരിക്കണം.

ഇനി കാര്യത്തിലേക്ക് കടക്കാം. നമ്മെ ചെറിയ ക്ലാസുകളില്‍ എണ്ണാന്‍ പഠിപ്പിക്കും. എണ്ണൽ സംഖ്യകളെ കൂട്ടാനും  കുറയ്ക്കാനുമൊക്കെ പഠിച്ചു കഴിയുമ്പോൾ ഭിന്ന സംഖ്യകൾ പഠിപ്പിക്കും. തുടർന്ന് അഭിന്നകങ്ങൾ ,നെഗറ്റീവ് സംഖ്യകൾ എന്നിങ്ങനെ പലതരം സംഖ്യകളെ പരിചയപ്പെടുത്തും. കുറേകൂടി മുതിർന്ന ക്‌ളാസിൽ ഒരു വര  വരച്ച് അതില്‍ വിവിധ തരം സംഖ്യകളെ അടയാളപ്പെടുത്താൻ  പഠിപ്പിക്കും. നെഗറ്റീവ് സംഖ്യകള്‍, ഭിന്നകങ്ങള്‍(rational), അഭിന്നകങ്ങള്‍(irrational) എന്നിങ്ങനെ എല്ലാത്തരം റിയല്‍ നമ്പരുകളേയും സംഖ്യാരേഖയിൽ (number line) രേഖപ്പെടുത്താം. സംഖ്യാരേഖയുടെ  നടുക്കാണ് പൂജ്യം ഇരിക്കുന്നത് എന്നുവേണമെങ്കിൽ വിചാരിക്കാം.  പൂജ്യത്തിന് ഇടതു വശത്ത് നെഗറ്റീവുകളും വലത്ത് പോസിറ്റിവുകളും ഇരിക്കുന്നു. സംഖ്യാരേഖയിലുള്ള ഓരോ ബിന്ദുവിനും പൂജ്യത്തിൽ നിന്നുള്ള ദൂരമാണ് ആ ബിന്ദുവിന്റെ വിലയായി അടയാളപ്പെടുത്തുന്നത്. ഇങ്ങനെ രേഖപ്പെടുത്തുന്ന വിലകളെ നമുക്ക്  സ്കേലാർ (scalar ) എന്ന് വിളിക്കാം (ചിത്രം 2) സ്കേലാറുകൾ കേവലം സംഖ്യകൾ മാത്രമാണ്. സംഖ്യാരേഖയിൽ ഇവ പൂജ്യത്തിനു ഇടത്തോ  വലത്തോ  എന്ന് കാണിക്കാൻ  പോസിറ്റീവ് നെഗറ്റീവ് ചിഹ്നങ്ങൾ ഉപയോഗിക്കും.

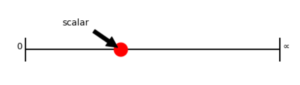ചിത്രം 2

 

കുറെക്കൂടി വലിയ ക്ലാസില്‍ നമ്മെ  ജോമെട്രി പഠിപ്പിക്കും. ജോമെട്രിക്കൽ രുപങ്ങൾ വരക്കുന്നത് ഒരു പ്രതലത്തിൽ (plane)  ആണ്. ഇതിനുവേണ്ടി നമുക്ക് പ്രതലത്തിലെ ഓരോ ബിന്ദുവിനെയും കൃത്യമായി അടയാളപ്പെടുത്തേണ്ടതുണ്ട്.   പ്രതലത്തെ  പരസ്പരം ലംബമായ രണ്ട് നമ്പര്‍ ലൈനുകളുപയോഗിച്ച്  നാലായി തിരിക്കും. കാർട്ടീഷ്യൻ കോർഡിനേറ്റ്  സിസ്റ്റം എന്നാണ് ഈ പദ്ധതിയെ വിളിക്കുന്നത് രണ്ടു dimension  (2D)  ഉള്ള  ഏതു പ്രതലത്തെയും ഈ രീതി ഉപയോഗിച്ച് വിവരിക്കാം. ലിനിയർ ആൾജിബ്രായിൽ ഇതിനെ 2 D സ്പേസ് എന്നു വിളിക്കും.

ഇത് എളുപ്പത്തില്‍ മനസ്സിലാക്കുന്നതിന് നമുക്ക്  ചിത്രം 3ലെ  2D പ്രതലം എടുക്കാം. x,y എന്നിങ്ങനെ രണ്ട് ആക്സിസുകളാണ് ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്നത്.  ഈ പ്രതലത്തിലെ ഓരോ ബിന്ദുവിനും രണ്ടു കോർഡിനേറ്റുകളുണ്ട് .  x കോർഡിനേറ്റ് ബിന്ദുവിന് x ആക്സിസിൽ നിന്നുള്ള അകലത്തെ  സൂചിപ്പിക്കുന്നു. ഇതു പോലെ y കോർഡിനേറ്റ് Y ആക്സിസിൽ നിന്നുള്ള ദൂരത്തേയും. ഈ രീതിയിൽ നമുക്ക് പ്രതലത്തിലെ  ഏതൊരു ബിന്ദുവിനെയും കൃത്യമായി അടയാളപ്പെടുത്താൻ  കഴിയും. ഉദാഹരണമായി (10,10)  ഈ പ്രതലത്തിലെ ഒരു ബിന്ദുവാണ് . x ആക്സിസിൽ നിന്ന് 10 യൂണിറ്റും y ആക്സിസിൽ നിന്ന് 10 യൂണിറ്റും അകലെയാണു് ഈ ബിന്ദു ഇരിക്കുന്നത് .

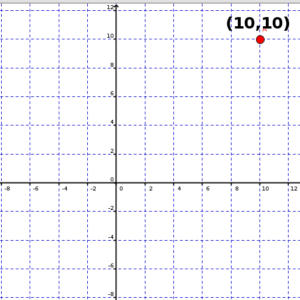
ചിത്രം 3

പ്രതലത്തിലെ ബിന്ദുക്കളെ മറ്റൊരു രീതിയിൽ കൂടിയും രേഖപ്പെടുത്താം. ഓരോ ബിന്ദുവിനും പൂജ്യത്തിൽ നിന്ന് കൃത്യമായ ദൂരം ഉണ്ട്. കൂടാതെ ഓരോ ബിന്ദുവിനും ഒരു ദിശ കൂടിയുണ്ട് . ഈ പ്രതലത്തിലെ ഏതൊരു  പോയിന്റിനേയുും ഈ സംവിധാനമുപയോഗിച്ച് രേഖപ്പെടുത്താം. ഉദാഹരണത്തിന് ചിത്രം 4ല്‍ 10,10 എന്ന പോയിന്റ് കാണിച്ചിരിക്കുന്നു. ഈ ബിന്ദു X ആക്സിസിൽ നിന്ന് നാൽപ്പത്തഞ്ച് ഡിഗ്രി മാറി പുജ്യത്തിൽ നിന്ന് 14.4 യൂണിറ്റ് അകലെയാണ് ഉള്ളത്.

 

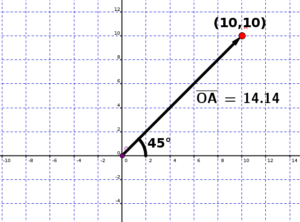
ചിത്രം 4

ദിശയും പൂജ്യത്തിൽ നിന്നുള്ള ദൂരവും ഉപയോഗിച്ചും നമുക്ക് ബിന്ദുക്കളെ രേഖപെടുത്താം . ചിത്രം 5 നോക്കിയാൽ ഈ രേഖപ്പെടുത്തൽ രീതി കുറേക്കൂടി വ്യക്തമാകും. ചിത്രത്തിൽ പൂജ്യത്തിൽ നിന്ന്  നാല് ബിന്ദുക്കളിലേക്ക്  വരകൾ കാണിച്ചിട്ടുണ്ട്. ഓരോ വരയിലുമുള്ള ആരോ മാർക്ക് ഒരു ദിശ കാണിക്കുന്നു.  ആ പോയിന്റ് പൂജ്യത്തിൽ നിന്ന് എത്ര ദൂരെയാണ് എന്നത് വരയുടെ നീളത്തിലുള്ളത്  . ഇങ്ങനെ രേഖപ്പെടുത്തുന്ന ഓരോ ബിന്ദുവും  ഓരോ വെക്ടര്‍ ആണെന്ന് പറയാം. അതായത് ഓരോ  വെക്റ്ററും ഒരു ദിശയെ സൂചിപ്പിക്കുന്നു. കൂടാതെ ഓരോ വെക്റ്ററിനും   (0,0) എന്ന മൂലബിന്ദുവില്‍ നിന്ന് നിശ്ചിത ദൂരവുമുണ്ട്.

ഇങ്ങനെ നോക്കിയാല്‍ ഈ പ്രതലം നിറയെ വെക്ടറുകളാണ്. കാർട്ടീഷ്യൻ കോർഡിനേറ്റ് ഉപയോഗിച്ചും ചിത്രത്തിൽ കാണിച്ചതു പോലെ ദിശ ഉപയോഗിച്ചും നമുക്ക് വെക്ടറുകളെ അടയാളപ്പെടുത്താം. (10,10) എന്ന വെക്ടറിനെ ചിത്രം നാലിൽ ഈ രണ്ടു രീതിയിലും അടയാളപ്പെടുത്തിയിട്ടുണ്ട് .  പക്ഷെ കംപ്യൂട്ടര്‍കളിൽ എളുപ്പത്തിൽ വെക്ടറുകളെ രേഖപെടുത്താവുന്നതു കോർഡിനേറ്റുകൾ ഉപയോഗിച്ചുള്ള രീതിയിലാണ്.

ഇനി നമുക്ക് മൂന്നോ നാലോ വെക്ടറുകളെ രേഖപ്പെടുത്തണമെന്നിരിക്കട്ടെ. അവയുടെ കോര്‍ഡിനേറ്റുകളെ നിരത്തി എഴുതാം. ഉദാഹരണത്തിന് (10,10),  (10,20),  (4,-6),  (-14,8) എന്നീ വെക്ടറുകളെ പരിഗണിക്കുക (ചിത്രം 5 ). ഇവയൊക്കെ വെക്ടറുകളാണ്.  പകരം  ചിത്രം 6 ൽ കാണിച്ചിരിക്കുന്നത് പോലെ  ഒരു മെട്രിക്സായി   എഴുതാം.  ഇവിടെ ഓരോ വരിയും (row ) ഓരോ വെക്റ്റർ ആണ്.(ഇത് റോ ക്ക് പകരം കോളം എന്ന് തിരിച്ചുവേണമെങ്കിലും എടുക്കാം.. കൂടുതൽ അറിയേണ്ടവർ ഏതെങ്കിലും ലീനിയർ ആൾജിബ്ര പുസ്‌തകം നോക്കുന്നത് നന്നായിരിക്കും.)

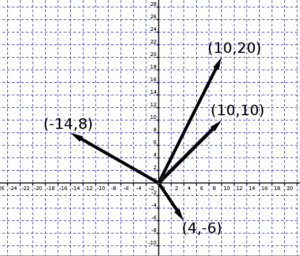
ചിത്രം 5

 

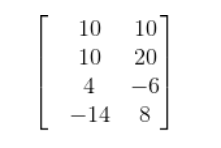
ചിത്രം 6

സ്കൂളിൽ നമ്മൾ മെട്രിക് സുകളെ കൂട്ടുന്നതിനും  കുറയ്ക്കുന്നതിനുമൊക്കെ പഠിച്ചിട്ടുണ്ടാകും. യഥാർത്ഥത്തിൽ രണ്ട് മെട്രിക്സുകളെ തമ്മില്‍ കൂട്ടുന്നത്  വെക്ടറുകള്‍ തമ്മില്‍ കൂട്ടുന്നതിന് തുല്യമാണ്. ചിത്രം 7 ല്‍ ഒരു ഉദാഹരണം  കാണിച്ചിരിക്കുന്നു.

 

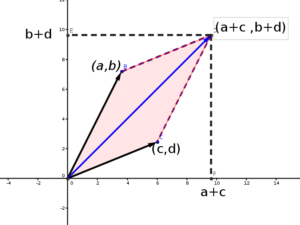
ചിത്രം 7

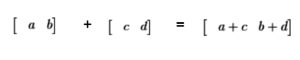
ചിത്രം 7a

 മറ്റ് മെട്രിക്സു ഓപറേഷനുകളും ഇതുപോലെ വിശദീകരിക്കാന്‍ പറ്റും.മെട്രിക്സുകൾ ഉപയോഗിച്ചാൽ പല വെക്റ്റർ ഓപ്പറേഷനുകളും വളരെ എളുപ്പത്തിൽ ചെയ്യാം.

ചിത്രം 8

ഇനി നമുക്ക്  ത്രിമാന ജോമേട്രി പരിഗണിക്കാം ഇവിടെ  ഓരോ  ബിന്ദുവിനും മൂന്ന് കോര്‍ഡിനേറ്റ്കള്‍ വീതമുണ്ട്. x,y,z എന്നിങ്ങനെ. ലീനിയർ അൽജിബ്രയിൽ നമ്മൾ ഇതിനെ ഒരു 3d  സ്പേസ് എന്ന് വിളിക്കും. (ചിത്രം 8)

ഈ സ്പേസിലുള്ള ഒരുകൂട്ടം വെക്ടറുകളെ രേഖപ്പെടുത്തണമെങ്കില്‍ നമുക്ക് മെട്രിക്സ് ഉപയോഗിക്കാം. ഉദാഹരണം താഴെയുണ്ട്. (ചിത്രം 9)

ചിത്രം 9

ഇവിടെയും ഓരോ നിരയും (row ) ഓരോ   വെക്ടറാണ്.

നമുക്ക് മൂന്ന് ‍‍ഡൈവെന്‍ഷന്‍ വരെയെ വിഷ്വലൈസ് ചെയ്യാനുള്ള കഴിവുള്ളൂ. എന്നാല്‍ മൂന്നിലധികം ഡൈമെന്‍ഷെന്‍ ഉള്ള സ്പേസുകളേക്കുറിച്ച് ആലോചിച്ചിട്ടുണ്ടോ. ഉദാഹരണത്തിന് സമയത്തെ ഒരു ഡൈമെന്‍ഷെനായി എടുത്താല്‍   3Dയില്‍ ഉള്ള നമ്മുടെ ഭൂമി സമയത്തിലൂടെ നിങ്ങിക്കൊണ്ടിരിക്കുകയാണ്. ഇതിനെ നമുക്ക് നാലാമത് ഒരു സംഖ്യക്കൊണ്ട് രേഖപ്പെടുത്താം. മെട്രിക്സിന്റെ ഓരോ  റോയിലും നാലു വീതം സംഖ്യകളുണ്ടാകും. ആദ്യത്തേ മൂന്നണ്ണം നമ്മുടെ x,y,zഉം നാലമത്തേത് സമയവും.

ഇതുപോലെ മറ്റ് ഉയര്‍ന്ന ഡൈമെന്‍ഷനുകള്‍ സാധ്യമാണ്. ഇത്തരം നിരവധി ഡൈമെന്‍ഷനല്‍  ഉള്ള സ്പേസുകളെക്കുറിച്ചുള്ള പഠനമാണ് ലീനിയര്‍ ഓള്‍ജിബ്രാ.  ഇത്തരം സ്പേസുകളെ വളരെ എളുപ്പത്തിൽ നമക്ക്‌ മെട്രിക്സ് രൂപത്തിൽ എഴുതാം. കൂടാതെ  ഈ സ്പേസുകളിൽ ഉള്ള വെക്ടറുകയുടെ സ്വഭാവം പഠിക്കാനും മെട്രിക്സ് ഉപയോഗിക്കാം  മെട്രിക്സിലെ ഓരോ റോയും ഈ സ്പേസിലെ വെക്ടറുകളായി കരുതാം (നമുക്ക് തിരിച്ചും രേഖപ്പെടുത്താം ഓരോ കോളവും ഒരു  വെക്ടര്‍ എന്ന ക്രമത്തില്‍.)മെട്രിക്സുകളെ N ഡയമെൻഷനൽ സ്പേസിലെ ബിന്ദുക്കളെ അടയാളപ്പെടുത്താനുള്ള എളുപ്പവഴിയായിക്കരുതാം.ഇത്തരം സ്പേസിൽ ഓറോബിന്ദുവിനും N കോർഡിനേറ്റുകൾ ഉണ്ടാകും

ഇനി നമ്മുടെ 2Dപടത്തിലേക്ക്  (ചിത്രം 3 ) തിരിച്ചു വരാം. ഇതിലെ x,y അക്സിസുകളും വെക്ടറുകളാണ്.  ഇവരെ ബേസിസ് വെക്ടര്‍ എന്ന് വിളിക്കുന്നത് (യഥാര്‍ത്ഥത്തില്‍ ബേസിസ് വെക്ടറുകള്‍ പരസ്പരം ലംബമാകണമെന്ന് നിര്‍ബന്ധമില്ല).

ഇനി മെട്രിക്സുകളുടെ ഒരു പ്രായോഗിക ഉപയോഗം പരിചയപ്പെടുത്താം .   മെഷീന്‍ ലേണിംഗിലും മറ്റും നമുക്ക് തിരിച്ചറിയേണ്ട വസ്തുക്കളുടെ ഫീച്ചറുകള്‍ ഓരോന്നും കണ്ടുപിടിച്ച് വലിയ വെക്ടറാക്കി മാറ്റും. എത്ര ഫീച്ചറുണ്ടോ അത്രയും ഡൈമെന്‍ഷന്‍ ഉള്ള ഒരു സ്പേസിലെ പോയിന്റായിട്ടാകും ഓരോ വസ്തുവിനേയും കരുതുക. ഈ സ്പേസിലാകും നമ്മുടെ അല്‍ഗോരിതങ്ങള്‍ പ്രവര്‍ത്തിക്കുന്നത്.ഇതിനെക്കുറിച്ച് പിന്നീട് എഴുതാം.

ലീനിയർ അൾജിബ്രയെക്കുറിച്ചു കൂടുതൽ അറിയാൻ എം ഐ ടി പ്രൊഫസർ ആയ ഗിൽബെർട്  സ്ട്രാങ്ന്റെ  പുസ്തകവും വിഡിയോ ലക്ച്ചറുകളും ലഭ്യമാണ് ലിങ്ക് ഇവിടെ. https://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/   കുറെക്കൂടി ലളിതമായി ഈ ലിങ്കിലെ വിഡിയോ ഇതൊക്ക വിശദീകരിച്ചിട്ടുണ്ട് https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab

ചിത്രങ്ങൾ വരച്ചത് വിദ്യ സുനിൽ.